 Process
Analysis Toolkit (PAT) 3.5
Help Process
Analysis Toolkit (PAT) 3.5
Help |
PAT's CSP# module supports a rich modeling language named CSP#(pronounced
'CSP sharp', short for Communicating Sequential Programs) which combines
high-level modeling operators like (conditional or non-deterministic) choices,
interrupt, (alphabetized) parallel composition, interleaving, hiding,
asynchronous message passing channel, etc., with programmer-favored low-level
constructs like variables, arrays, if-then-else, while, etc.. It offers great
flexibility on how to model your systems. For instance, communication among
processes can be either based on shared memory (using global variables) or
message passing (using asynchronous message passing or CSP-style multi-party
barrier synchronization). The high-level operators are based on the
classic process algebra Communicating
Sequential Processes (CSP). Our design principle for CSP# is to
maximally keep the original CSP as a sub-language of CSP#, whilst offering a
connection to the data states and executable data operations. The above illustrates the work flow of the CSP Module. System analysis in PAT
is supported in two ways, namely, simulation or model checking. The visualized
simulator allows the users to interactively play with their models, by choosing
one of the enabled actions at a time, let the computer to generate system traces
randomly or even build the complete state graph (given it is not very large).
The model checkers embedded in PAT are designed to apply state-of-the-art model
checking techniques for systematic analysis. Users can state assertions in
various forms, and by just clicking one button, PAT would tell whether the
assertion is true or not (in which case a counterexample is generated and ready
to be simulated). PAT has a number of different model checking algorithms for
efficient verification of different properties. For instance, an efficient
depth-first-algorithm is used to verify safety properties by identifying a bad
state, an SCC-based algorithm is used to verify liveness properties by
identifying a bad loop and an SCC-based algorithm to verify liveness properties
under fairness by identifying a fair bad loop (refer to our
paper [SUNLDP09] for detail). CSP module is distinguished in a number of aspects from existing model
checkers. In the following, we briefly introduce the two of them. To reveal the
full details, please refer to our publications. The LTL model checking algorithm in PAT is designed to handle a variety of
fairness constraints efficiently. This is partly motivated by recently developed
population protocols, which only work under weak, strong local/global fairness.
The other motivation is that the current practice of verification is deficient
under fairness. Two different approaches for verification under fairness are
supported in PAT, targeting different users. For ordinary users, one of the
following options may be chosen and applied to the whole system: weak fairness
or strong local/global fairness. The model checking algorithm works by
identifying the fair execution at a time and checks whether the desirable
property is satisfied. Notice that unfair executions are considered unrealistic
and therefore are not considered as counterexamples. Because of the fairness,
nested depth-first-search is not feasible and therefore the algorithm is based
on an improved version of Tarjan's algorithm for identifying strongly connected
components. We have successfully applied it to prove or disprove (with a
counterexample) a range of systems where fairness is essential. In general,
however, system level fairness may sometimes be overwhelming. The worst case
complexity is high and, much worse, partial order reduction is not feasible for
model checking under strong local/global fairness. A typical scenario for
network protocols is that fairness constraints are associated with only
messaging but not local actions. We thus support an alternative approach, which
allows users annotate individual actions with fairness. Notice that this option
is only for advanced users who know exactly which part of the system needs
fairness constraints. Nevertheless this approach is much more flexible, i.e.,
different parts of the system may have different fairness. Furthermore, it
allows partial order reduction over actions which are irrelevant to the fairness
constraints, which allows us to handle much larger systems. LTL formulas assert properties over each and every single execution of the
system, PAT allows users to reason about behaviors of a system as a whole by
refinement checking. Refinement checking is to verify whether an
implementation's behaviors follow the specifications. PAT supports six notions
of refinements based on different semantics, namely trace refinement, stable
failures refinement, failures divergence refinement and each of the above
refinement augmented with data refinement. A refinement checking algorithm
(inspired by the one implemented in FDR but extended with partial order
reduction) is used to perform refinement checking on-the-fly. Refinement
checking in FDR only compares the traces (e.g., event sequences) of the
implementation and the specification. For practical systems (other than those
specified with process algebra), it may be desirable to also compare the data
structures. For instance, linearizability is an important correctness criteria
for concurrent data structure. Informally, it requires that the data structure
accessed by multiple processes concurrently must be updated as if the processes
access it sequentially. To establish a refinement relationship, not only the
event of accessing the data structure must be compared between a sequential
specification and a concurrent implementation, but also the data structure
itself must be checked. We thus provide a user option to state whether to check
for data refinement.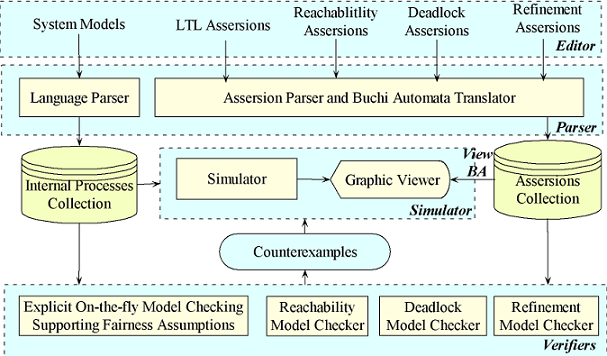
Copyright © 2007-2012 Semantic Engineering Pte. Ltd.